Four Fundamental subspaces

This is a one of several posts in Linear Algebra series. All the posts are available here. I assume you are familiar with basics of Vector Spaces and Subspaces if not refer Vector Spaces and Subspaces.

In this post we will dive into Independence, Span, Basis, and Dimension of a vector. Finally we will look into Four fundamental subspaces.

Linear Independence

Vectors $\vec{x_1}, \vec{x_2}, …, \vec{x_n}$ are independent if no combination gives zero vector except the zero combination. That is, $Ax = 0$ only when $x = 0$. Also, we know that Null space $N(A)$ has all the solutions when $Ax = 0$, the columns are independent if N(A) contains only the zero vector.

In contrast to this, the columns are dependent exactly when there is a nonzero vector in the null space. Another way to see linear dependence is: “One vector is a combination of the other vectors.” Let’s see how dependent and independent vectors looks like:

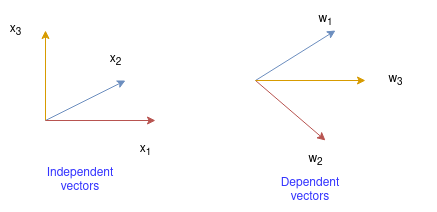
Here the vectors $\vec{x_3}$ adds new dimension to the plane formed by $\vec{x_1}$ and $\vec{x_2}$, so $\vec{x_1}, \vec{x_2}, \vec{x_3}$ are independent vectors. But $\vec{w_3}$ lies in the same plane as $\vec{w_1}$ and $\vec{w_2}$, so $\vec{w_1}, \vec{w_2}, \vec{w_3}$ are dependent vectors.

Now let’s see how linear dependence relates to the rank of a matrix.

\[A = \begin{bmatrix} 1& 2& 2 & 2 \\ 2& 4& 6& 8 \\ 3 & 6 & 8 & 10\end{bmatrix}\] \[U = \begin{bmatrix} 1& 2 & 2 & 2 \\ 0 & 0 & 2 & 4 \\ 0& 0& 0& 0 \end{bmatrix}\]

Here the rank of A is 2. The columns are dependent as $C_2 = 2C_1$ and $C_4 = -2C_1 + 2 C_2$.

If we look at another example,

\[B = \begin{bmatrix}1 & 1 & 3\\ 7& 4 & 5 \\ 1 & 1 & 2\end{bmatrix}\] \[U = \begin{bmatrix}1 & 1 & 3\\ 0& 3 & 16 \\ 0 & 0 & 1\end{bmatrix}\]

Here the rank is 3. And the columns are independent.

So what we notice here is if rank $r = n$ then the columns are independent.

Vectors that Span a Subspace

Vectors $v_1, v_2, v_3, … , v_n$ span a space if the space consists of all linear combinations of those vectors.

For example:

\(v_1 = \begin{bmatrix}1 \\ 0\end{bmatrix}\) and \(v_2 = \begin{bmatrix}0 \\ 1\end{bmatrix}\) span the whole 2-D space in $\mathbb{R}^2$.

Basis for Vector Space

A basis for a vector is a sequence of vectors $v_1, v_2, v_3, … , v_n$ with two properties:

1. They are independent.
2. They span the space.

For example: In \(I = \begin{bmatrix}1 & 0\\ 0 & 1\end{bmatrix}\), \(i = \begin{bmatrix}1 \\ 0\end{bmatrix}\) and \(j = \begin{bmatrix}0 \\ 1\end{bmatrix}\) are independent and they span $\mathbb{R}^2$. So $I$ produce standard basis for $\mathbb{R}^2$.

So what is the basis for column space of $A$ in the previous example we discussed ?

For $A$, the basis are vectors \(\begin{bmatrix}1 \\ 2 \\ 3\end{bmatrix}\) and \(\begin{bmatrix}2 \\ 6 \\ 8\end{bmatrix}\) for it’s column space and they are actually our pivot columns. So the basis for column space are the pivot columns.

Dimension of a Vector Space

The dimension of a space is the number of vectors in every basis. For example there are two vectors in the basis of $A$ (same old example), so the dimension of column space of $A$ is $2$. In fact these two are the rank of the matrix. Ultimately we can say, dimension of the column space = rank of the matrix = number of pivot columns.

Similarly, the dimension of Null space is the number of free variable. So the dimension of Null space of A is 2.

Bases of Matrices

Until now we have talked about column space and row space which are made by a linear combination of columns vectors and row vectors but there is another form of vector space and that is matrix space. For example, all 2*2 matrices give space M and matrices inside M satisfy rules i.e. we can add them, multiply them by a scalar, some combination of matrices might give zero matrices. Subspace of the matrix space M are symmetric matrices, upper triangular matrices, diagonal matrices.

One of the basis for 2*2 matrices is $A_1$, $A_2$, $A_3$, $A_4$ \(\begin{bmatrix}1 & 0\\ 0 & 0\end{bmatrix}\) , \(\begin{bmatrix}0 & 1\\ 0 & 0\end{bmatrix}\) , \(\begin{bmatrix}0 & 0\\ 1 & 0\end{bmatrix}\) , \(\begin{bmatrix}0 & 0\\ 0 & 1\end{bmatrix}\)

These matrices are linearly independent as we are seeing the entire matrix not just a single column and a linear combination of these bases will span the entire matrix space.

Combination of basis matrices $c_1A_1+c_1A_1+c_1A_1+c_1A_1$ = \(\begin{bmatrix}c_1 & c_2\\ c_3 & c_4\end{bmatrix}\) = $A$

A is zero only if the c’s are all zero and this proves independence of $A_1$, $A_2$, $A_3$, $A_4$. The three matrices $A_1$, $A_2$, $A_4$ are a basis for a subspace-the upper triangular matrices. Its dimension is 3. $A_1$ and $A_4$ are a basis for the diagonal matrices. What is a basis for the symmetric matrices? Keep $A_1$ and $A_4$ , and throw in $A_2$+$A_3$.

To push this further, think about the space of all n by n matrices. One possible basis uses matrices that have only a single nonzero entry (that entry is 1). There are $n^2$ positions for that 1, so there are $n^2$ basis matrices and the dimension is $n^2$. Similarly dimension of the subspace of symmetric and upper triangular matrices is $\frac{1}{2} n^2+\frac{1}{2} n$. The dimension of the subspace of Diagonal matrices is $n$

Four fundamental subspaces

As we already know, subspaces can be described in two ways: a set of vectors that span the space (example: The Columns span the column space) and the space that satisfy certain conditions (example: Null space consists of all vectors that satisfy Ax = 0.)

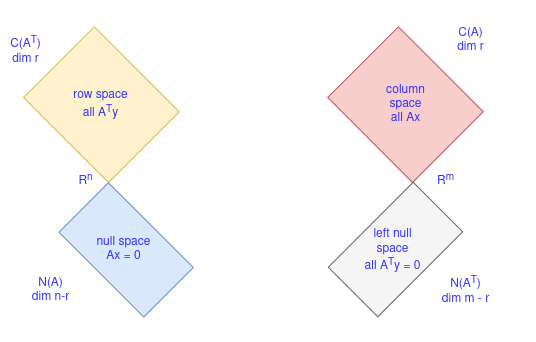
The four fundamental subspaces are:

1. Row space, $C(A^T)$:

   The row space of A is the column space of $A^T$. For the echelon matrix U obtained from A in our example above, the row space is all combinations of rows. And we can see that the last row contributes nothing. The first two rows are the basis for the row space. So the nonzero rows are basis and the row space has dimension r. As we perform elimination, we do not change row space so $A$ has the same dimension $r$ as the row space of $U$. It has the same bases. Basis for row space is first r rows of R where R is row reduce echelon form of A.

2. Column space, $C(A)$:

   If we look at this space from domain and range view, we see that C(A) is the range (set of all possible values $f(x)$; $x$ is in the domain). So our function is $f(x) = Ax$ and has domain all $x$ in $R^n$.

   Columns $C_1$ and $C_3$ of $U$ are the basis for its column space as they are the pivot columns. This is true for A as well even though they have different column space. The dimension of the column space is rank $r$ which equals the dimension of the row space. The number of independent columns equals the number of independent rows. Performing elimination on matrix changes Columns space i.e $C(U)\not ={}C(A)$.

3. Null space $N(A)$:

   The nullspace of $U$ has dimension = $n - r$. The special solutions are the basis. The nullspace of $A$ is the same as the nullspace of $U$ and $R$.

   The nullspace is also called the kernel of A, and its dimension $n-r$ is the nullity.

4. Left null space $N(A^T)$:

   As we know, dimension of $C(A)$ + dimension of $N(A)$ = number of columns.

   This is true for $A^T$ as well with m columns. So,

   dimension of $C(A^T)$ + dimension of $N(A^T)$ = m

   $\implies$ $r$ + dimension of $N(A)$ = $m$
   $\implies$ dimension of left null space $N(A^T) = m - r$.

Here is the summary of the four subspaces associated with $m$ by $n$ matrix $A$ of rank $r$.

m, n, r	dim R(A)	dim N(A)	dim C(A)	dim $N(A^T)$	solvability of $Ax = b$
$m = n = r$	$r$	$0$	$r$	$0$	solvable, ${\bf x}={\bf A}^{-1}{\bf b}$ is unique solution
$m > n = r$	$r$	$0$	$r$	$m - r$	solvable if ${\bf b}\in C({\bf A})$
$n > m = r$	$r$	$n - r$	$r$	$0$	solvable, infinite solutions ${\bf x}={\bf x}_p+N({\bf A})$
$r < min(m,n)$	$r$	$n - r$	$r$	$m - r$	solvable only if ${\bf b}\in C({\bf A})$, infinite solutions

Example: \(A = \begin{bmatrix}1 & 2 \\ 3 & 6\end{bmatrix}\) has m = n = 2, and rank $r = 1$.

1. The column space has all multiples of \(\begin{bmatrix}1\\3\end{bmatrix}\).
2. The row space contains all multiples of \(\begin{bmatrix}1\\2\end{bmatrix}\).
3. The null space contains all multiples of \(\begin{bmatrix}-2\\1\end{bmatrix}\)
4. The left nullspace contains all multiples of \(y = \begin{bmatrix}-3\\1\end{bmatrix}\). The rows of $A$ with coefficients $-3$ and $1$ add to zero, $A^Ty = 0$

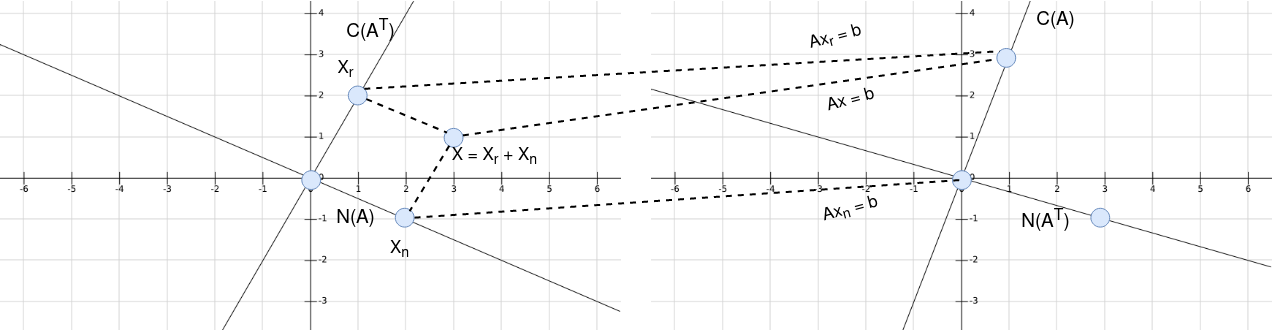
Here the row space $C(A^T)$ is the multiples of (1,2), the null space $N(A)$ is the multiples of $(2, -1)$, column space $C(A)$ is the multiples of $(1, 3)$ and left null space is the multiples of $(3, -1)$.

Also we can see that Row space is orthogonal to Null space and Column space is orthogonal to Left nullspace.

References

1. Introduction to Linear Algebra, W. G. Strang
2. The Fundamental Theorem of Linear Algebra
3. The Four Fundamental Subspaces