Ramer–Douglas–Peucker algorithm

The Problem

When we were working on a satellite image of one of the local area of Nepal, we had to simplify the obtained mask to feed into the GIS system. In order to simplify, we ended up using a very interesting yet simple algorithm, Ramer-Douglas-Peucker algorithm (also called Douglas-Peucker algorithm).

Here is a sample image and it’s corresponding masks:

Fig 1. Original sliced image

Fig 2. Masks of houses (left) and result after simplifying using RDP algorithm (right).

The Algorithm

In 1973, David H. Douglas and Thomas K. Peucker introduced an algorithm that produced a simplified polyline than the original in their paper: “Algorithms for the reduction of the number of points required to represent a digitized line or its caricature”. The algorithm generates a new curve similar to the original curve, but with fewer points.

The original paper defines the first point as anchor and last point as floater. All the remaining points are examined to find the one with the greatest perpendicular distance between the point and the line joining anchor and floater. If the distance is less than the tolerance defined, then all points are terminated and the straight line segment represents the whole line. Otherwise, the point with greatest distance is set as a new floater. The algorithm recursively calls itself with anchor and floaters and finally merges it to give the simplified polyline.

There is this simple gif from Mysid on RDP:

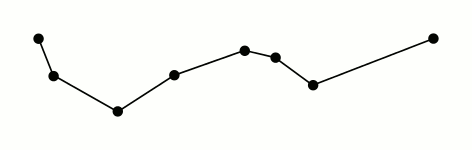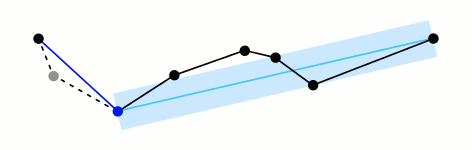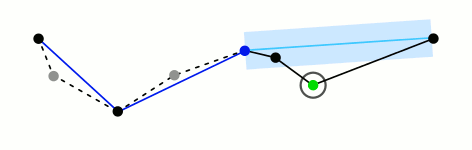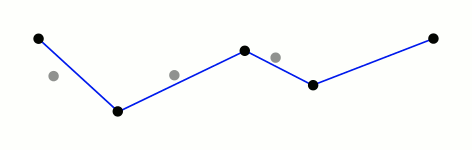
In the worst case, this algorithm has a running time of $O(n^2)$ and in the best case, it has running time of $O(nlog ⁡n)$. 2

Code

def perpendicular_distance(line, point):
   '''
   Parameters
   ----------
   line: list
       2D list containing end point of line
   point: list
       [x,y] co-oridinates from which perpendicualar distance is to be calculated

   Returns
       distance
   -------
   '''
   x1, y1 = line[0][0], line[0][1]
   x2, y2 = line[1][0], line[1][1]
   x, y = point[0], point[1]
   slope = (y2 - y1 + 1e-5) / (x2 - x1 + 1e-5)
   A = slope
   B = -1
   C = -A * x1 + y1
   perpendicular = (abs((A * x + B * y + C + 1e-5) / math.sqrt(A ** 2 + B ** 2 + 1e-5)))
   return perpendicular

def douglasPeuckar(pointList, epsilon):
   '''
   Parameters
   ----------
   pointList: list
       2D list of point of curve
   epsilon: float
       tolerance
   Returns: list
       2D list of points of new curve
   -------
   '''
   dmax = 0
   index = 0
   end = len(pointList)
   for i in range(1, end):
       # previous point to last index
       d = perpendicular_distance([pointList[0], pointList[end - 1]], pointList[i])
       if d > dmax:
           index = i
           dmax = d
   resultList = []
   if dmax > epsilon:
       rec_result1 = douglasPeuckar(pointList[0:index], epsilon)
       rec_result2 = douglasPeuckar(pointList[index:end], epsilon)
       resultList.extend(rec_result1)
       resultList.extend(rec_result2)
   else:
       resultList = [pointList[0], pointList[end - 1]]
   return resultList

Here are some results from the above code:

Blue line: Original curve

Orange line: Result

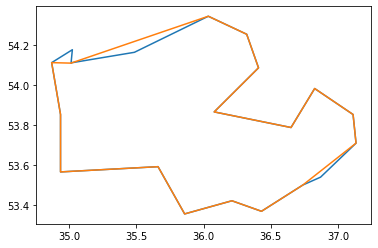
Fig 3. RDP result for epsilon=0.1

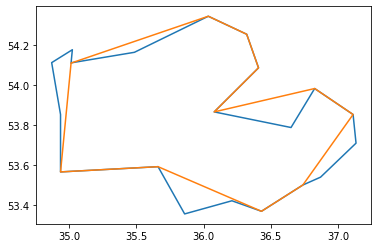
Fig 4. RDP result for epsilon=0.2

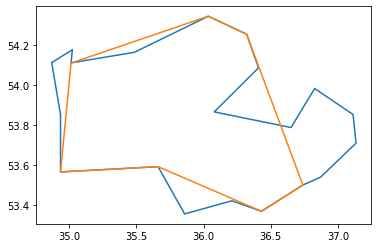
Fig 5. RDP result for epsilon=0.5

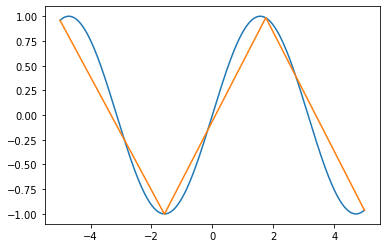
Fig 6. RDP result for sin function

Co-Authors: Shital Adhikari and Anil Kumar Shrestha

Resources

1. Douglas, D. H., & Peucker, T. K. (1973). Algorithms for the reduction of the number of points required to represent a digitized line or its caricature.
2. Wikipedia
3. Wu et al. A non-self-intersection Douglas-Peucker algorithm. https://www.dca.fee.unicamp.br/~ting/Publications/P2001-2005/wu-roci-2003-rfm.pdf
4. https://rdp.readthedocs.io