Determinants

This is one of several posts in Linear Algebra series. All the posts are available here.

This post will briefly walk you through the determinants, its properties, Cramer’s rule and some applications of determinants.

Overview

If $A$ = [$a_{ij}$] is a square matrix of order $n$, then we can associate a number (complex or real) called determinant of matrix $A$, written as det $A$ or $|A|$. The determinants are defined only for square matrices. So if we have a square matrix

\[A = \begin{bmatrix} a & b \\ c & d \\ \end{bmatrix}\]

then the determinant of $A$ is:

\[|A| = \begin{vmatrix} a & b\\ c & d\\ \end{vmatrix} = ad - bc\]

The determinant encodes a lot of information about the matrix. The matrix $A$ is invertible exactly when the determinant is non-zero and hence we can solve $Ax = b$. When $A$ is invertible, the determinant of $A^{-1}$ is $\dfrac{1}{det A}$.

Interestingly, the sign of the determinant tells us the nature of the transformation associated with the matrix. For example: multiplying a unit square matrix with a matrix with negative determinant

\[\begin{bmatrix} -2 & 0\\ 0 &-2 \\ \end{bmatrix}\]

scales and transformers the matrix. (Explained in detail here ).

Properties of the determinant

1. The determinant of an Identity matrix is 1. $det I = 1$

   \[\begin{vmatrix} 1 & 0\\ 0 & 1 \end{vmatrix} = 1 \qquad \begin{vmatrix} 1\\ & .\\ && .\\ &&& .\\ &&&& 1\\ \end{vmatrix} = 1\]

2. If we exchange two rows of a matrix, the sign of the determinant gets reversed.

   \[\begin{vmatrix} a & b\\ c & d\\ \end{vmatrix} = - \begin{vmatrix} c &d\\ a & b \end{vmatrix}\]

3. (a) If we multiply one row of a matrix by $t$, the determinant is multiplied by $t$.

\[\begin{vmatrix} ta & tb \\ c & d \end{vmatrix} = t \begin{vmatrix} a & b\\ c & d \end{vmatrix}\]

(b) The determinant behaves like a linear function on the rows of the matrix.

\[\begin{vmatrix} a + a' & b + b' \\ c & d\\ \end{vmatrix} = \begin{vmatrix} a & b\\ c & d \end{vmatrix} \begin{vmatrix} a' & b'\\ c & d \end{vmatrix}\]

Rest of the properties can be deduced from these three properties.

1. If two rows of a matrix, $A$ are equal, $det A$ is zero.

   \[\begin{vmatrix} a & b\\ a & b \end{vmatrix} = ab - ab = 0\]

2. If we subtract a multiple of one row from another row, $det A$ does not change.

   \[\begin{vmatrix} a & b\\ c - la & d - lb \end{vmatrix} = \begin{vmatrix} a & b\\ c & d \end{vmatrix} - \begin{vmatrix} a & b\\ tc & td\\ \end{vmatrix} \\ = \begin{vmatrix} a & b\\ c & d \end{vmatrix} - t \begin{vmatrix} a & b\\ a & b \end{vmatrix} \\ = \begin{vmatrix} a & b\\ c & d \end{vmatrix}\]

3. If $A$ has a row that is all zeros, then $det A$ = 0.

   \[\begin{vmatrix} 0 & 0\\ c & d \end{vmatrix} = 0\]

4. If $A$ is a triangular matrix then det A = product of diagonals (pivots) = $d_1, d_2, d_3,…, d_n$.

   \[\begin{vmatrix} d_1 & 0\\ 0 & d_2 \end{vmatrix} = (d_1)(d_2)\]

5. If $A$ is singular then det A = 0. If A is invertible then $det A$ $\not ={0}$.

   If $A$ is singular, we can get zero row by elimination and hence by property $6$, $det A = 0$.

6. Determinant $|AB| = |A||B|$

   From this we get,

   \(det A^{-1} = \dfrac{1}{detA}\) as $(det A)(det A^{-1}) = det I = 1$

7. $det A^T = det A$

   \[\begin{vmatrix} a & b\\ c & d \end{vmatrix} = \begin{vmatrix} a & c\\ b & d \end{vmatrix} = ad - bc\]

Determinant of an $n$ by $n$ matrix can be found in three ways:

1. Pivot formula: multiply the $n$ pivots
2. Big formula: add up $n!$ terms
3. Cofactor formula: Combine $n$ smallet determinants

The Pivot Formula

Here the determinant is simply the multiples of pivots for $A = LU$.

\[(det P)(det A) = (det L)(det U) \implies det A = \pm (d_1, d_2, ... , d_n)\]

where the determinant of $P$ is $-1$ or $+1$. The odd number of row exchanges means $det P = -1$ and even as $det P = +1$.

Example:

\[A = \begin{bmatrix} 0 & 0 & 2\\ 0 & 1 & 7 \\ 3 & 2 & 11 \end{bmatrix}\]

row exchange gives:

\[A = \begin{bmatrix} 3 & 2 & 11\\ 0 & 1 & 7 \\ 0 & 0 & 2 \end{bmatrix}\]

so $det A = -(3)(1)(2) = -6$

The Big Formula for Determinants

This gives us the explicit formula for the determinant rather directly from $a_{ij}$. So we can pluck the values of $a_{ij}$’s to get the determinant.

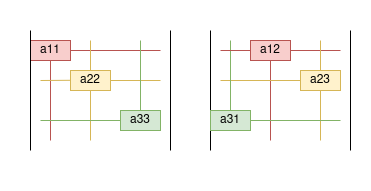
Let’s take an example of a $3 \times 3$ matrix. Here we have $3! = 6$ ways to order the columns and hence we have $6$ determinants.

\[\begin{vmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{vmatrix} = \begin{vmatrix} a_{11} \\ &a_{22}\\ &&a_{33}\\ \end{vmatrix} + \begin{vmatrix} &a_{12} \\ &&a_{23}\\ a_{31}\\ \end{vmatrix} + \begin{vmatrix} &&a_{13} \\ a_{21}\\ &a_{32}\\ \end{vmatrix} + \\ \begin{vmatrix} a_{11} \\ &&a_{23}\\ &a_{32}\\ \end{vmatrix} + \begin{vmatrix} &a_{12} \\ a_{21}\\ &&a_{33}\\ \end{vmatrix} + \begin{vmatrix} &&a_{13} \\ &a_{22}\\ a_{31}\\ \end{vmatrix}\]

Here we are taking one entry from every row and column.

In general,

$det A$ = sum of all $n!$ column permutations $P = (\alpha, \beta, …, \omega)$

$= \sum(det P)a_{1\alpha},a_{2\beta}…a_{n,\omega}$

Determinant by Cofactors

Here we are taking one entry from each row and column and finding its cofactors.

Let us suppose,

\[\begin{vmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{vmatrix} = \begin{vmatrix} a_{11} \\ & a_{22} & a_{23}\\ & a_{32} & a_{33}\\ \end{vmatrix} + \begin{vmatrix} & a_{12} & \\ a_{21} & & a_{23}\\ a_{31} & & a_{33}\\ \end{vmatrix} + \begin{vmatrix} & & a_{13}\\ a_{21} & a_{22} & \\ a_{31} & a_{32} & \\ \end{vmatrix}\]

then the determinant is: $a_{11}C_{11} + a_{12}C_{12} + a_{13}C_{13}$ where $C_{11}, C_{12}, C_{13}$ are cofactors.

\[C_{11} = \begin{vmatrix} a_{22} & a_{23}\\ a_{32} & a_{33}\\ \end{vmatrix} , C_{12} = \begin{vmatrix} a_{21} & a_{23}\\ a_{31} & a_{33}\\ \end{vmatrix} , C_{13} = \begin{vmatrix} a_{21} & a_{22} \\ a_{31} & a_{32} \\ \end{vmatrix}\]

And the sign of these cofactors are determined by $(-1)^{i + j}$, where $i, j$ are $i^{th}$ row and $j^{th}$ column.

Cramer’s Rule

Cramer’s rule involves the use of determinants to find the solution. With Cramer’s rule we can find the value of $x$, $y$, or $z$ individually. We don’t need the values of $x$ and $y$ to find the value of $x$. For $3\times3$ matrix $A$ and $Ax = b$, it looks like:

\[x = \dfrac{D_x}{D}, y = \dfrac{D_y}{D}, z = \dfrac{D_z}{D}\]

where

\[D_x = \begin{vmatrix} b_1 & a_{12} & a_{13}\\ b_2 & a_{22} & a_{23}\\ b_3 & a_{32} & a_{33}\\ \end{vmatrix} D_y = \begin{vmatrix} a_{1,1} & b_1 & a_{13}\\ a_{1,2} & b_2 & a_{23}\\ a_{1,3} & b_3 & a_{33}\\ \end{vmatrix} D_z = \begin{vmatrix} a_{1,1} & a_{1,2} & b_1\\ a_{1,2} & a_{2,2} & b_2\\ a_{1,3} & a_{3,2} & b_3\\ \end{vmatrix}\]

Once we find these, we can calculate $x$, $y$ and $z$ by using Cramer’s rule mentioned above.

A simple example:

\[-x + 3y -2z = 5\\ 4x - y - 3z = -8\\ 2x + 2y -5z = 7\]

Here, \(D = \begin{vmatrix} -1 & 3& -2\\ 4 & -1 & -3\\ 2 & 2 & -5 \end{vmatrix} = -39 - (-50) = 11\)

\[D_x = \begin{vmatrix} 5 & 3& -2\\ -8 & -1 & -3\\ 7 & 2 & -5 \end{vmatrix} = -6 - 104 = -110\] \[D_y = \begin{vmatrix} -1 & 5& -2\\ 4 & -8 & -3\\ 2 & 7 & -5 \end{vmatrix} = -126 - (-47) = -79\] \[D_z = \begin{vmatrix} -1 & 3& 5\\ 4 & -1 & -8\\ 2 & 2 & 7 \end{vmatrix} = -1 - (-90) = -91\]

Finally using Cramer’s rule,

\[x = \dfrac{D_x}{D} = \dfrac{-110}{11} = -10\] \[y = \dfrac{D_y}{D} = \dfrac{-79}{11} = \dfrac{-79}{11}\] \[z = \dfrac{D_z}{D} = \dfrac{-91}{11} = \dfrac{-91}{11}\]

Applications

1. Check linear independence: If the determinant of a matrix is zero, the columns/rows of vectors of a matrix is linearly dependent.
2. Orientation of a basis: If determinant of $A$ is positive, $A$ preserves orientation, where as if it is negative, $A$ changes the orientation of the basis.
3. Solve $Ax = b$.
4. Determinant gives the area of a parallelogram
5. Determinant gives the volume of a box
6. Determinant gives the triple product $(\vec{u} \times \vec{u}). \vec{w}$

References

1. Introduction to Linear Algebra, W. G. Strang
2. Properties of determinant (MIT)
3. Matrices and Determinants
4. The Determinant (hadrienj)
5. Using Cramer’s Rule to Solve Three Equations with Three Unknowns