How does volumetric integration work?

Volumetric Integration is one of the well-known and established algorithms in surface reconstruction. The long-term success of this method can be attributed to its robustness, efficiency, resilience and incremental nature. These features have meant that modern frameworks such as Open3D has leaned on utilizing it for their sophisticated surface reconstruction pipeline.

The core idea of this method is to generate an iso-surface by integrating a bunch of range images using weighted summation of signed distance functions, allowing mesh extraction using methods such as the marching-cubes algorithm.

Table of Contents

---

1) Key Terms 2) Algorithm 3) Merits 4) References

---

Key Terms

• Range and Depth Images
  The range and depth images are pictoral representation of 3D information captured by a depth sensing camera. To store various levels of range/depth, each pixel of the image are assigned a different intensity. The only fundamental difference between the two types of representations is that a range image represents the distances between the observed points and the depth sensor, while a depth image represents the distances perpendicular to the sensor plane.
• Voxel
  A Voxel (volumetric pixel) is a three-dimensional reprisentation of a point in a grid. Just like a pixel (Picture Element) that represents a point in two dimensional space (picture) using two co-ordinates, a voxel does the same but using three co-ordinates.
• Signed Distance Function (SDF)
  Signed Distance Function (SDF) of a voxel is the distance between its center and the nearest object surface in the direction of current measurement (ray between the camera and the voxel).
  The SDF is positive infront of a surface (in free space), heighest value being right infront of the camera, and is negative behind (inside) the surface.
  

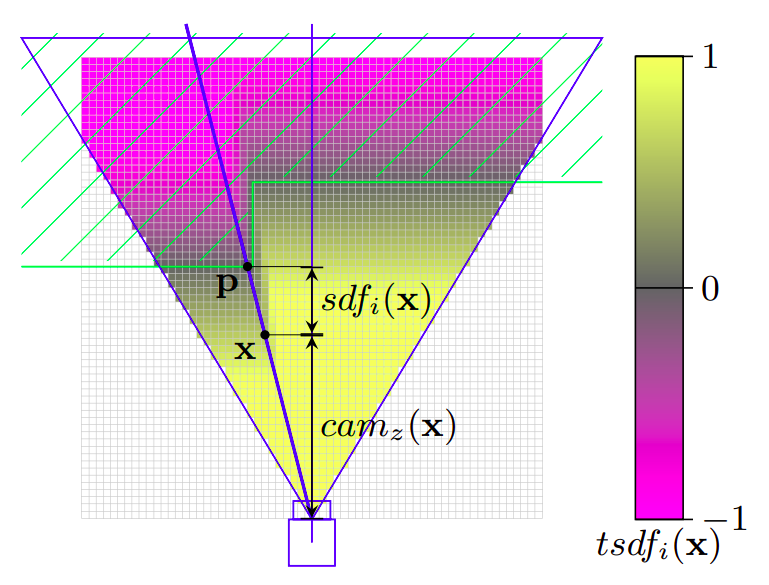
Fig 1: Signed Distance of a voxel x for the shown camera

As shown in the Fig 1, for the ith observation, the signed distance value of a voxel x can be computed as

sdf_i(x) = depth_i(pic(x)) - cam_z(x)

pic(x) is the projection of the voxel center x onto the depth image. So depth_i(pic(x)) is the measured depth in between the camera and the nearest object surface point p on the viewing ray crossing x. Accordingly, cam_z(x) is the distance in between the voxel and the camera along the optical axis. Note that sdf is also measured along the optical axis of the camera.

• Truncated Signed Distance Function (TSDF)
  For the purpose of surface reconstruction, the signed-distance values are normalized/truncated because large distances are not relevant in this case. Thus they are called Truncated Signed Distance Function (TSDF).

tsdf_i(x) = max (-1, min(1,sdf_i(x)/t))

• Zero-Crossing
  The Zero-Crossing for a voxel, along the ray of measurement, is the point in the voxel grid in which the signed distance function changes from positive to negative.
• Iso-Surface
  An iso-surface is a surface of points of constant value within a volume of three-dimensional space. It is analogous to an iso-line in two-dimensional area. The equation of an iso-surface would be f(x,y,z) = c.
• Implicit Functions
  Implicit functions are the functions that are defined by associating one of the variables with the others. Such functions can be used to define a iso-surface as follows

z = f(x,y)
so, z - f(x,y) = 0

Algorithm

The entire field-of-view accross a set of range images is represented by a voxel grid, the main goal is to approximate where a surface lies in this grid, combining the information given by these images. Each voxel in the grid can be assigned a signed-distance value and a weight value by the signed distance function and the weight function respectively.

The algorithm is summarized as follows

• Each voxel is initialized with a weight of zero, which will eventually be overwritten by updated values
• Each range image is tesellated by constructing triangles from the neareast neighbors on the sampled lattice. This gives a continuous surface from a discrete range image.
• Weights are computed at each vertex of the triangle mesh by taking a dot product between each vertex normal and viewing direction (indicating greater uncertainty when the illumination is at grazing angles to the surface). Now, we have a triangle mesh with a weight at each vertex.
• A signed distance contribution is computed for each voxel in the sensor’s field-of-view by casting rays from the sensor through the voxels’ centers, and then intersecting them with the triangle mesh.
• Weight for the voxel is computed by linearly interpolating the weights of the intersection triangle’s vertices.
• With the new weight and signed distance, the weight and signed distance are updated as follows

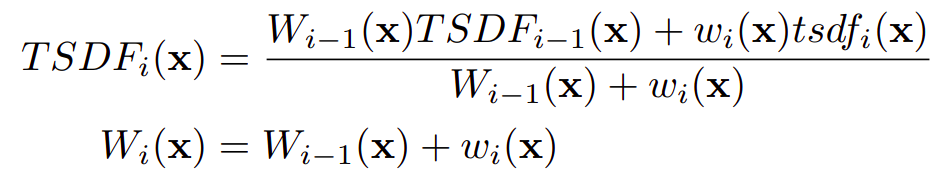
• Once all the range images are used to compute and update the weights and signed distance values for each voxel, the zero crossing can be determined to obtain an overall iso-surface.
• Finally, a refined mesh surface without redundancy and overlapping can be obtained by using marching cubes algorithm from the obtained iso-surface.

Merits

This volumetric integration method is a sampled-state implicit algorithm that utilizes structured data. It has several merits over the parametric approaches and other implicit approaches, such as

• It utilizes useful information such as surface normal and viewing angles, thus is robust in regions of high curvature, and in presence of systematic distortions and outliers.
• It uses continuous data from triangulation and thus is able to represent range uncertainty by the means of weights, as opposed to discrete data algorithms.
• It is able to combine and correct the noisy and overlapping range images by incremental updation, making it resilient to such errors.
• It is optimized for computation time and space efficiency since multiple sets of range images can be integrated in parallel.
• It offers an inherent technique for whole filling, and has already been used along with even better techniques along the years.

References

Curless, B., Levoy, M.: A volumetric method for building complex models from range images. In: Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH 1996, pp. 303–312. ACM, New York (1996)

Werner, D., Al-Hamadi, A., Werner, P.: Truncated signed distance function: experiments on voxel size. In: Proceedings of the International Conference Image Analysis and Recognition, Springer (2014), pp. 357-36

Authors: Aashutosh, Madhav